Geometria: problemi svolti sui triangoli

  • Autore: Antonio Guadagno
  • Fonte: Seneta.it

In un triangolo isoscele ABC, il segmento AH è l’altezza relativa alla base BC e K è la proiezione del punto H sul lato obliquo AC.
Sapendo che AK misura 17,6 cm e KC misura 9,9 cm, calcolare l’area e il perimetro del triangolo.

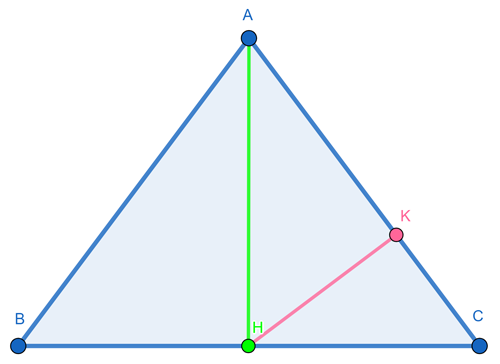
Triangolo Isoscele Euclide

AC = AK + KC ⟹ AC = 17,6 + 9,9 = 27,5cm

Applicando il Primo Teorema di Euclide al triangolo AHC si ha:
AC : HC = HC : KC ⟹ HC2 = AC ⋅ KC
AC : AH = AH : AK ⟹ HC2 = AC⋅ AK

HC2 = 27,5 ⋅ 9,9 = 272,25 ⟹ HC = 16,5cm
AH2 = 27,5 ⋅ 17,6 = 484 ⟹ AH = 22cm

BC = 2 ⋅ HC ⟹ BC = 33cm

Il perimetro è pari a:
2p = 2 ⋅ AC + BC ⟹ 2p = 2 ⋅ 27,5 + 33 = 88cm
L’area è pari a:
A = (AH ⋅BC)/2 ⟹ A = (22 ⋅ 33 )/2 = 363cm2

Visite: 26637

Pagine: 1 2 3 4 5 6 7 8 9