Fisica – I moti nel piano: il moto dei proiettili con esercizi
Il moto di un proiettile
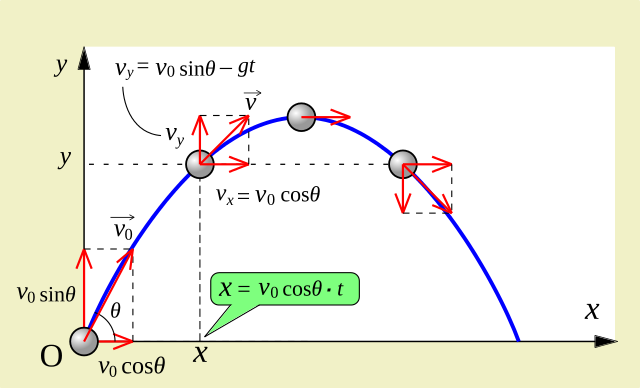
Si supponga di lanciare un oggetto da terra con una velocità \(\vec v_0\) e con inclinazione pari a \(\theta\) rispetto all’asse orizzontale.
Naturalmente, al variare del modulo \(v_0\) della velocità e dell’angolo \(\theta\) di inclinazione l’oggetto cadrà più o meno lontano, percorrendo la cosiddetta gittata d, ovvero la distanza orizzontale a partire dal punto di lancio.
La velocità iniziale può essere scomposta nelle sue componenti orizzontale e verticale \(v_{0x}=v_0cos\theta\) e \(v_{0y}=v_0sen\theta\).
Durante il movimento le due componenti della velocità sono:
$$ v_x=v_{0x}=v_0cos\theta $$ $$v_y=v_{0x}-gt=v_0sen\theta-gt$$
Allo stesso modo, anche il moto dell’oggetto può essere scomposto nelle due direzioni, orizzontale e verticale, lungo le quali è rispettivamente rettilineo uniforme e rettilineo uniformemente accelerato (per effetto dell’attrazione terrestre). In particolare:
$$ x=v_{0x}t=v_0cos\theta t $$ $$y=v_{0y}t-\displaystyle\frac{1}{2}gt^2=v_0sen\theta t-\displaystyle\frac{1}{2}gt^2$$
Ricavando il tempo dalla prima equazione e sostituendolo nella seconda:
$$t=\displaystyle\frac{x}{v_0cos\theta} \Rightarrow y=\displaystyle\frac{v_0xsen\theta}{v_0cos\theta}- \displaystyle\frac{gx^2}{2{v_0}^2cos^2\theta}$$
$$ y= -\displaystyle\frac{g}{2{v_0}^2cos^2\theta} x^2 +tan\theta \cdot x $$
Esprimendo infine \(y\) in funzione di \(x\), si ottiene una parabola con la concavità rivolta verso il basso (coefficiente di \(x^2\) negativo) e passante per l’origine degli assi.
In altre parole il corpo parete con una traiettoria inclinata dell’angolo \(\theta\), perdendo gradualmente quota a causa dell’accelerazione di gravità. L’altezza massima raggiunta (trascurando la resistenza dell’aria) rappresenta il punto medio della gittata e il tempo di volo si divide equamente tra il tempo di ascesa e quello di discesa.
Per calcolare la gittata occorre porre \(y=0\) nell’equazione della parabola, ottenendo:
$$\displaystyle\frac{g}{2{v_0}^2cos^2\theta} x^2=tan\theta \cdot x \Rightarrow x=\displaystyle\frac{2{v_0}^2cos\theta sen\theta}{g}$$
da cui si ottienne il valore della gittata:
$$d=\displaystyle\frac{{v_0}^2 sen2\theta}{g}$$
Il valore della gittata assume il valore massimo quando \(sen2\theta=1\), ovvero quando \(\theta=45°\); di conseguenza: $$d_{max}=\displaystyle\frac{{v_0}^2}{g}$$
Per calcolare l’altezza massima, ricordando che essa ha per ascissa la metà della gittata, è sufficiente sostituire il valore \(d/2\) nell’equazione della parabola:
$$h=-\displaystyle\frac{g}{2{v_0}^2 cos^2\theta} \cdot \left(\displaystyle\frac{{v_0}^2sen2\theta}{2g}\right)^2+tan\theta \left(\displaystyle\frac{{v_0}^2sen2\theta}{2g}\right)$$
Sviluppando i calcoli si ottiene:
$$ h=\displaystyle\frac{{v_0}^2 sen^2\theta}{2g} $$
Nel caso di gittata massima si ha: $$ h=\displaystyle\frac{{v_0}^2}{4g} $$
Visite: 10249
