Fisica – I moti nel piano: il moto circolare uniforme con esercizi
La velocità angolare
Nel Sistema Internazionale le ampiezze degli angoli sono misurate in radianti (rad).
Come nella figura seguente, l’ampiezza \(\alpha\), espressa in radianti, è il rapporto tra la lunghezza \(l\) dell’arco e il raggio \(r\) della circonferenza, cioè il modulo di \(\vec r\): $$\alpha=\displaystyle\frac{l}{r}$$
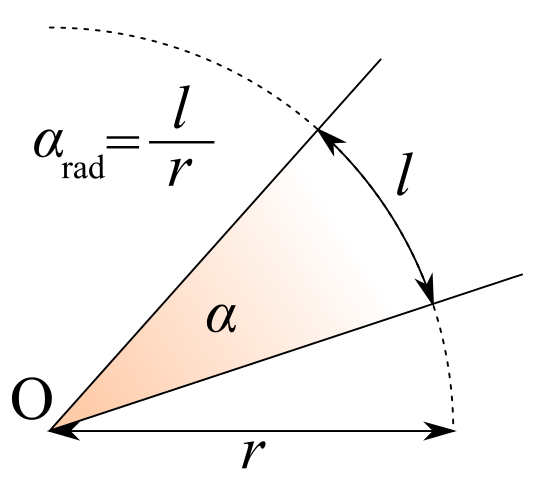
Si definisce spostamento angolare \(\alpha\) l’ampiezza dell’angolo al centro spazzato dal raggio vettore da un punto materiale che si muove lungo una circonferenza.
In altre parole, mentre un punto materiale si muove lungo una circonferenza di centro O e percorre un arco di lunghezza \(l\),il suo raggio vettore \(\vec r\) spazza un angolo di ampiezza \(\alpha\).
Partendo dallo spostamento angolare si può definire la velocità angolare.
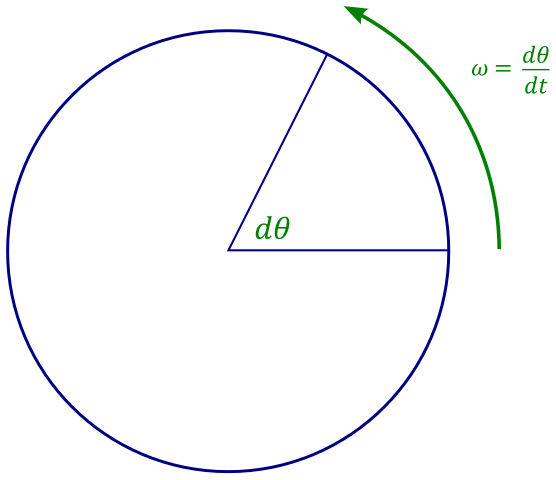
Si definisce velocità angolare \(\omega\) di un punto materiale che si muove di moto circolare uniforme il rapporto fra l’angolo percorso \(\Delta\theta\), misurato in radianti, e l’intervallo di tempo \(\Delta t\) impiegato per percorrerlo: $$ \omega=\displaystyle\frac{\Delta\theta}{\Delta t} $$
In particolare, essendo \(\omega\) costante, scegliendo come angolo l’angolo giro \(2\pi\) e come durata il periodo \(T\) si ha:
$$ \omega=\displaystyle\frac{2\pi}{T} \Leftrightarrow \omega=2\pi f$$
Ricordando che $$v=\displaystyle\frac{2\pi r}{T}$$ è possibile mettere in relazione il il modulo della velocità e la velocità angolare:
$$v=\omega \cdot r$$
Visite: 32190
