Matematica: le disequazioni di II grado fratte con esercizi svolti
Risolvere la seguente disequazione:
$$\displaystyle\frac{x^3-4x^2-x+4}{x^4+3x^2-4}\ge0$$
$$\displaystyle\frac{x^2(x-4)-(x-4)}{(x^-1)(x^2+4)}\ge0$$
$$\displaystyle\frac{(x^2-1)(x-4)}{(x^2-1)(x^2+4)}\ge0$$
$$\displaystyle\frac{x-4}{(x^2+4)}\ge0$$
Per quanto riguarda il numeratore si ha un’equazione di primo grado:
\(x-4\ge0\), ovvero: \(x\ge 4\).
Per quanto riguarda il denominatore, essendo una somma di quadrati, assume sempre valori positivi.
Dal punto di vista grafico si ha:
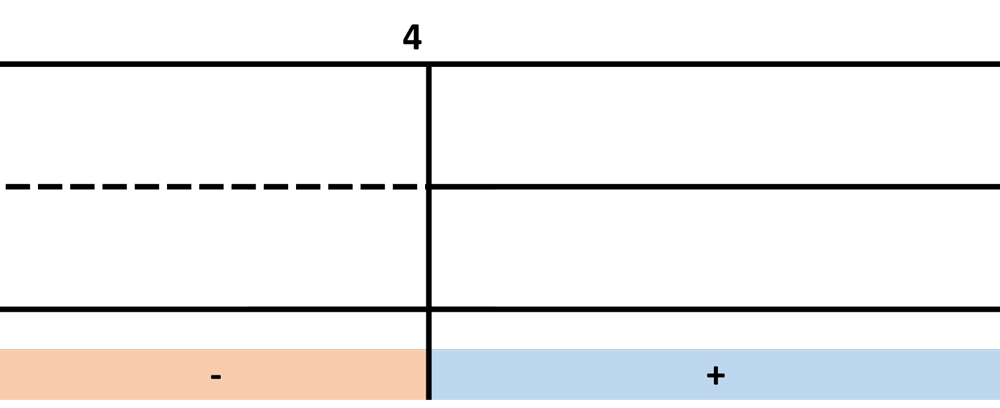
La disequazione è quindi verificata per:
$$x\ge 4$$
Visite: 80617
sabato 20 Marzo - 2021
