Numeri complessi: Generalità
Rappresentazione esponenziale
La rappresentazione esponenziale si basa sull’equazione di Eulero \(e^{i\theta}=\cos \theta+i \sin \theta\) che mette in relazione l’esponenziale di un numero immaginario con la rappresentazione trigonometrica dei numeri complessi. In particolare:
$$ z=x+iy=\rho(cos \theta + i sin \theta)=\rho e^{i\theta} $$
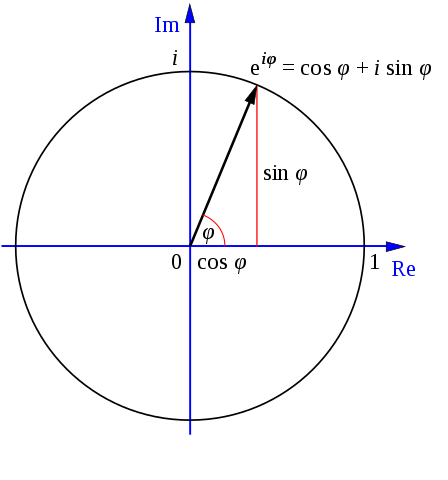
La rappresentazione esponenziale è utilizzata spesso per risolvere equazioni
in cui sono presenti essenzialmente le operazioni di prodotto, divisione e potenze.
Esempio.
\(z=i \Rightarrow x=0, y=1 \Rightarrow \)
\(\rho=\sqrt{0^2+1^2}=1\) e \(\theta=\arctan \left( \frac{1}{0} \right)=\frac{\pi}{2} \Rightarrow\)
\(z=e^{i\frac{\pi}{2}}\)
Esercizio.
\( \frac{i \sqrt{3}+i)}{(i-1)} =\sqrt{2}e^{i\pi{\frac{11}{12}}} \) poiché
\( i=e^{i\frac{\pi}{2}} \;\;\;\;(\sqrt{3}+i)=2e^{i\frac{\pi}{6}}\;\;\;\; (1-i)=\sqrt{2}e^{-i\frac{\pi}{4}} \)
Visite: 650
