• Autore: Antonio Guadagno
• Fonte: Seneta.it

Forma trigonometrica dei numeri complessi

Ogni punto $(x,y)$ del piano di Argand-Gauss può essere individuato anche assegnando la sua distanza $r$ dall’origine e l’angolo $\phi$ compreso tra il semiasse positivo delle ascisse e la semiretta che dall’origine passa per $(x,y)$. Ricordando la definizione di seno e coseno si ha:
$$x=r\cos \phi y=rsen\phi$$ Di conseguenza:
$$z=x+iy=r\cos \phi +irsen\phi =r(\cos \phi +isen\phi )$$

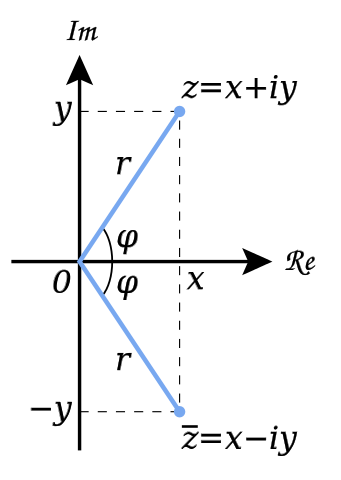
La rappresentazione $r(\cos \phi +isen\phi )$ prende il nome di forma trigonometrica del numero complesso $z=x+iy$.

$r=|z|$ prende il nome di modulo e $\phi =arg(z)$ prende il nome di argomento; $r$ e $\psi$ sono dette coordinate polari del punto $z$ nel piano complesso. In particolare:
$$\{\begin{array}{l}r=\sqrt{x^2+y^2}\\ \phi =\arctan (y/x)\end{array}$$

Se due o più numeri complessi hanno modulo uguale, allora saranno posizionati sulla stessa circonferenza con centro nell’origine; se hanno argomento uguale (a meno di multipli interi di $2\pi$) stanno sulla stessa semiretta che parte dall’origine.

La forma trigonometrica consente di calcolare in modo più semplice il prodotto di numeri complessi. Ad esempio, dati $z=r(\cos \psi +i\sin \psi )$ e $w=\rho (\cos \theta +i\sin \theta )$ si ha:
$z\cdot w=r(\cos \psi +i\sin \psi )\cdot \rho (\cos \theta +i\sin \theta )=$
$r\rho [(\cos \psi \cos \theta –\sin \psi \sin \theta )+i(\sin \psi \cos \theta +\cos \psi \sin \theta )]=$
$r\rho [\cos (\psi +\theta )+i\sin (\psi +\theta )]$

Di conseguenza, il prodotto di due numeri complessi ha per modulo il prodotto dei moduli $(r\rho )$ e per argomento la somma degli argomenti $(\psi +\theta )$.

Con ragionamenti analoghi si dimostra che il quoziente di due numeri complessi ha come modulo il quoziente dei moduli e come argomento la differenza degli argomenti. Ad esempio, dati $z=r(cos\psi +isin\psi )$ e $w=\rho (cos\theta +isin\theta )$ si ha:
$\frac{z}{w}=\frac{r}{\rho }[\cos (\psi –\theta )+i\sin (\psi –\theta )]$.

Visite: 650

Dispense Scolastiche, Dispense Scolastiche: Matematica, In evidenza, Scuola

Matematica, Scuole Secondarie di II grado, Seneta.it, Studenti, Università