Numeri complessi: Generalità
Rappresentazione nel piano di Argand-Gauss
Così come numeri reali sono in corrispondenza biunivoca con i punti della retta euclidea, analogamente, associando al numero della forma \(z = x + iy\) il punto di coordinate \((x, y)\), si realizza una corrispondenza biunivoca tra i numeri complessi e i punti del piano cartesiano (detto piano di Argand-Gauss).
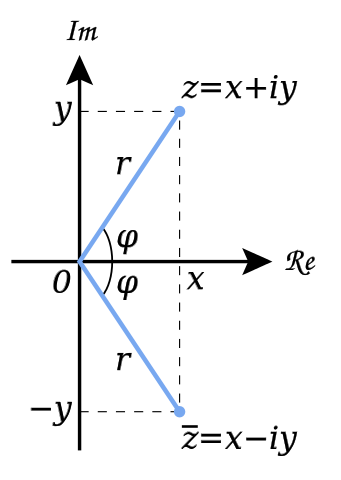
In tale corrispondenza: \(x = Re(z)\) rappresenta l’ascissa e \(y = Im(z)\) l’ordinata di \((x, y)\).
I numeri della forma \(x + 0i \) corrispondono ai punti dell’asse delle ascisse (detto appunto asse reale); i numeri della forma \(0+iy = iy\), detti immaginari puri, corrispondono ai punti dell’asse delle ordinate (detto asse immaginario).
Il valore di \(r\) in figura coincide con il modulo \(|z|=\sqrt{x^2+y^2}\) e rappresenta la distanza del punto \((x, y)\) dall’origine.
Visite: 650
