Numeri complessi: Generalità
Introduzione
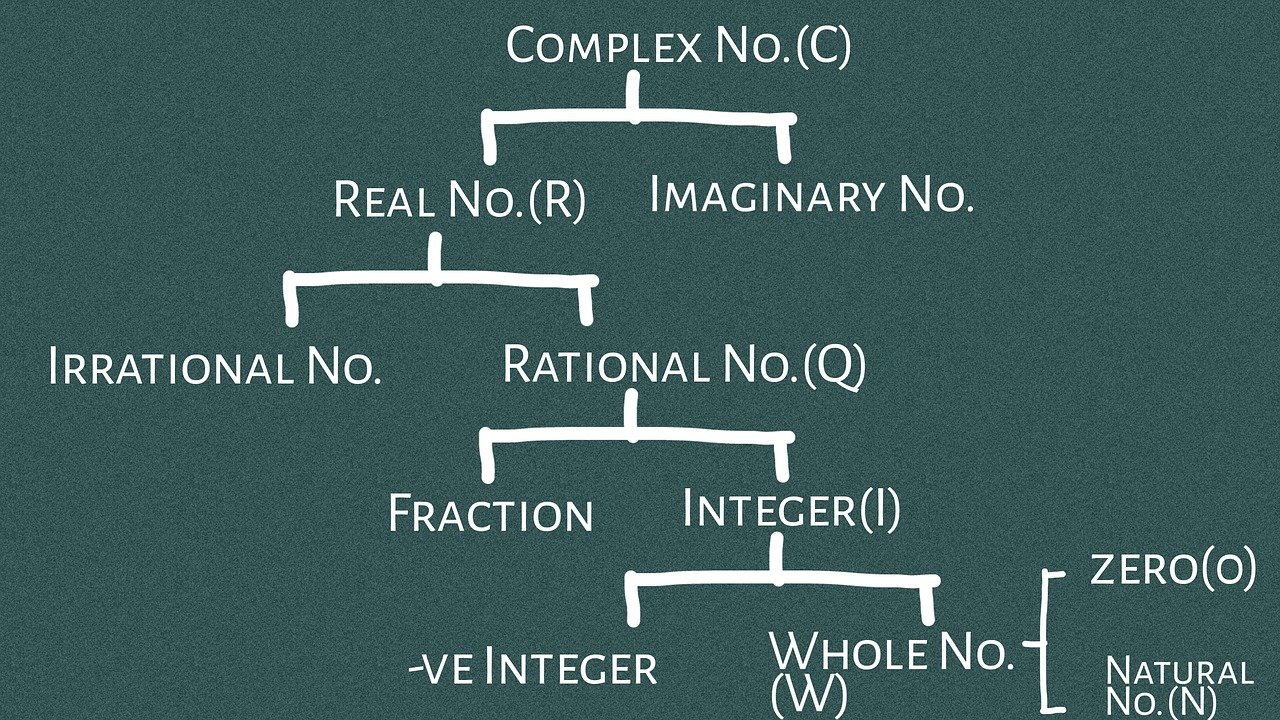
L’insieme dei numeri reali, definito come l’unione tra gli insiemi dei numeri razionali e dei numeri irrazionali, non è sufficiente a svolgere qualsiasi tipo di operazione; basti pensare a tutte le equazioni di secondo grado dotate di discriminante negativo (soluzioni complesse coniugate), come ad esempio come ad esempio \(x^2 +1 = 0\).
Per risolvere tale equazione si definisce allora il valore \(i\), chiamato unità immaginaria, tale che \(i^2=-1\) e quindi \(x^2=-1 \Rightarrow x= \pm i\).
Introduzione
Definizione di numero complesso
Operazioni nel campo dei numeri complessi
Rappresentazione nel piano di Argand-Gauss
Forma trigonometrica dei numeri complessi
La formula di de Moivre e le potenze di un numero complesso
Rappresentazione esponenziale
Radici n−esime di un numero complesso
Teorema fondamentale dell'algebra
Radici dell'unità
Visite: 650
