Matematica: introduzione alle funzioni
Funzioni inverse, crescenti, decrescenti e monotone
Sia \(f:A⟹B\) una funzione biunivoca (biettiva).
La funzione inversa di \(f\) è la funzione biunivoca \(f^{-1}: B \rightarrow A\) tale che: $$ f(x)= y ⟹ f^{-1}(y)=x\;\;\;\;\; f^{-1}(y)=x ⟹ f(x)= y $$
Sia data una funzione di \(X\) in \(\mathbb {R}\): \(f: (X) → (\mathbb {R})\).
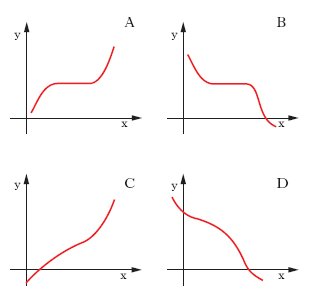
La funzione si dice crescente se: $$ \forall x_1, x_2 \in X : x_1 < x_2 ⟹ f(x_1) \le f(x_2) $$ La funzione si dice strettamente crescente se: $$ \forall x_1, x_2 \in X : x_1 < x_2 ⟹ f(x_1) < f(x_2) $$ La funzione si dice decrescente se: $$ \forall x_1, x_2 \in X : x_1 < x_2 ⟹ f(x_1) \ge f(x_2) $$ La funzione si dice strettamente decrescente se: $$ \forall x_1, x_2 \in X : x_1 < x_2 ⟹ f(x_1) > f(x_2) $$ Una funzione si dice monotona se è crescente o decrescente.
Visite: 4069
