• Autore: Antonio Guadagno
• Fonte: Seneta.it

Le funzioni

Le funzioni non sono altro che un caso particolare di relazioni nel quale ciascun elemento del primo insieme è in relazione con uno ed un solo elemento del secondo insieme.

Si definisce funzione \(f\) fra due insiemi \(A\) e \(B\) una relazione in cui ogni elemento di \(A\) associa uno e un solo elemento di \(B\). Poiché una funzione fa corrispondere a ogni elemento di \(A\) un unico elemento di \(B\), essa viene anche chiamata corrispondenza univoca. In simboli:
\(f: A → B\), che si legge: \(f\) è una funzione da \(A\) a \(B\).

Per indicare che a un elemento \(x\) di \(A\) corrisponde un elemento \(y\) di \(B\) si scrive: \(f: x → y\) oppure \(y = f(x)\), che si legge y uguale a effe di x.

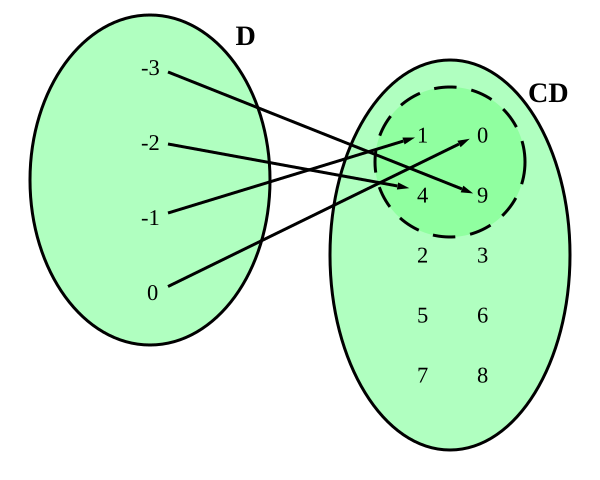
L’insieme di partenza A è detto dominio della funzione (e si indica con la lettera \(D\)); il sottoinsieme di B formato dalle immagini degli elementi di A è detto codominio della funzione (e si indica con la lettera \(C\) o \(y = f(x)\)).

Visite: 4069

Dispense Scolastiche, Dispense Scolastiche: Matematica, In evidenza, Pillole 2.0

Matematica, Scuole Secondarie di II grado, Seneta.it, Studenti, Università