Elementi di Teoria degli Insiemi
Operazioni sugli insiemi
Dati gli insiemi \(A\) e \(B\), le operazioni sugli insiemi che saranno trattate sono:
Unione |  |
Intersezione | 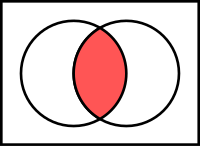 |
Differenza | 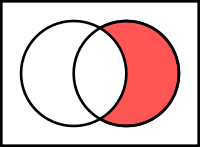 |
l’unione di \(A\) e \(B\) è l’insieme \(C\) degli elementi che appartengono ad \(A\) o a \(B\) e si indica con \(A \cup B\):
\(C=A \cup B = \{x\,|\;x \in A \;oppure\; x \in B \} \).
Se \(B \subseteq A \Rightarrow A \cup B = A \).
Inoltre: \(A \cup A=A\) (Idempotenza); \(A \cup \emptyset=A\).
l’intersezione di \(A\) e \(B\) è l’insieme \(C\) degli elementi che appartengono ad \(A\) e a \(B\) e si indica con \(A \cap B\):
\(C=A \cap B = \{x\,|\;x \in A \;e\; x \in B \} \).
Se \(B \subseteq A \Rightarrow A \cap B = B \).
Se \(A\) e \(B\) non hanno elementi comuni si dicono disgiunti e \( A \cap B = \emptyset \).
Inoltre: \(A \cap A=A\) (Idempotenza); \(A \cap \emptyset=\emptyset \).
la differenza fra \(A\) e \(B\), e si indica con \(B−A\) oppure \(B \setminus A\), è l’insieme \(C\) degli elementi che appartengono ad \(A\) ma non a \(B\):
\(C=A \cap B = \{x\,|\;x \in A \;e\; x \notin B \} \).
In particolare, se \(B \subseteq A\), \(B−A\) si dice complementare di \(B\) rispetto ad \(A\) e si indica con \(\overline{B}\).
Visite: 1283
