Pillole 2.0 – Algoritmo e Teorema di Böhm-Jacopini

  • Autore: Antonio Guadagno
  • Fonte: Seneta.it

La risoluzione dei problemi con l’ausilio dei computer è un processo che richiede un’analisi attenta, una pianificazione accurata e coerenza logica. Implica l’esecuzione di un insieme di istruzioni esplicite e non ambigue, espresse in un linguaggio di programmazione, il programma. Questo insieme di istruzioni molto semplici vanno sotto il nome di algoritmo.

Il concetto di algoritmo, in realtà, fa parte delle nostre azioni quotidiane, poiché ogni volta svolgiamo alcuni compiti anche banali (preparare un caffè, la risoluzione di un esercizio di geometria) che sono costituiti da elenco di passaggi da eseguire in maniera ordinata.

Concetto di Algoritmo

Questo insieme di istruzioni molto semplici è un esempio di algoritmo; quindi, un algoritmo è una sequenza di istruzioni perfettamente comprensibili ed eseguibili tali che, se eseguite in un ordine specificato e determinato, permettono la soluzione di un problema in un numero finito di passi.

Affinché una sequenza di istruzione possa essere considerata un algoritmo deve essere:
finita, cioè quando è costituito da un numero finito di istruzioni e presenta una fine;
deterministica, cioè quando partendo dagli stessi dati in input, si ottengono i medesimi risultati in output;
non ambigua, le operazioni devono poter essere interpretate nello stesso modo da tutti anche se l’esecutore è differente;
generale, cioè quando la soluzione è uguale per tutti i problemi della medesima classe.

Un algoritmo può essere rappresentato in modi diversi:

  1. con un linguaggio testuale, che può essere di vari tipi:
    – linguaggio di programmazione (Pascal, Java, C++, etc.);
    – linguaggio naturale (inglese, italiano);
    – pseudocodice (descrive a parole il compito svolto dall’algoritmo)
  2. con un linguaggio grafico (schema di flusso – Flow Chart), costituito da simboli grafici che rappresentano entità logiche diverse in relazione alla forma e consentono di rappresentare le azioni mediante composizione dei vari simboli secondo i differenti modelli logici.

Teorema di Böhm-Jacopini

Questo teorema ha un interesse essenzialmente teorico, in quanto i linguaggi di programmazione tendono ormai a dotarsi di istruzioni più complesse per evitare che i programmatori debbano occuparsi di istruzioni dispersive; in ogni caso, la sua attualità sta nel determinare strategie di programmazione “lineari, abolendo l’uso in passato delle istruzioni di salto incondizionato.

Il teorema di Böhm-Jacopini, enunciato nel 1966 da due informatici italiani, Corrado Böhm e Giuseppe Jacopini, dai quale prende il nome, afferma che:
"qualunque algoritmo può essere implementato utilizzando tre sole strutture, la sequenza, la selezione e il ciclo, da applicare ricorsivamente alla composizione di istruzioni elementari".

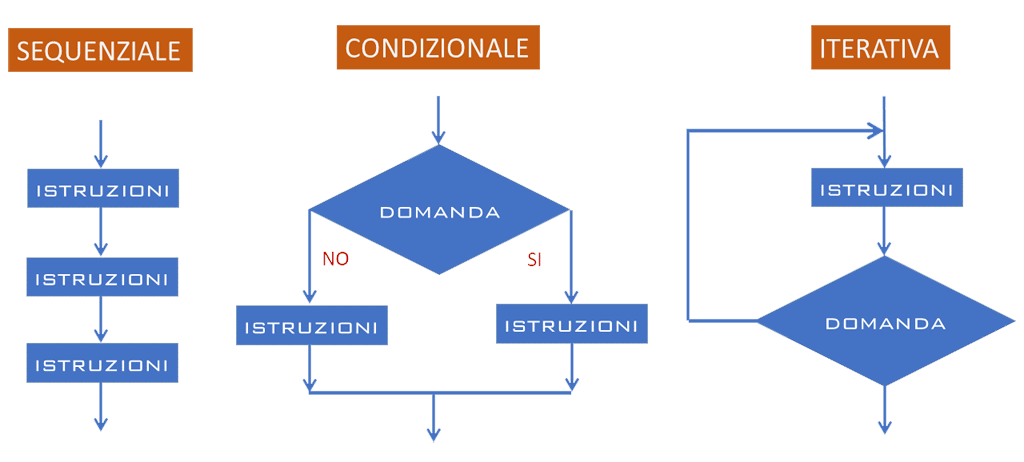
Gli schemi di composizione si suddividono quindi in tre tipi:

  1. Sequenza : le istruzioni sono eseguite secondo l’ordine in cui sono scritte; possono essere di tre tipi: lettura, scrittura, assegnazione.
  2. Selezione o Condizione : esiste una condizione da valutare e due possibili gruppi di istruzioni da eseguire; in funzione del valore della condizione, si sceglie un blocco oppure l’altro; per rappresentare la struttura condizionale, i linguaggi di programmazione usano la parole-chiave if, che può essere seguita da else («altrimenti») e da un end if.
  3. Iterazione : consente la ripetizione di un blocco di istruzioni, per un certo numero di volte, definito a seconda dell’obiettivo da raggiungere; quando si vuole iterare per un numero prestabilito di volte, si usa il ciclo di tipo for, in cui una variabile intera (Chiamata generalmente contatore) viene incrementata di una unità a ogni iterazione. Quando invece il numero di iterazioni non è noto a priori, si usa il ciclo di tipo while (controllo in testa) oppure il ciclo di tipo do (controllo in coda).
Selezione, Condizione, Iterazione

Visite: 10566